In Part 1 of this tutorial we looked at harmonizing the C Major scale with triad chords (chords that use 3 notes). In this second part of “Harmonizing the Major scale” we will look at how you can expand upon those triad chords to make use of extended chords (chords that use 4 or more notes) when harmonizing any Major scale.
If you play an instrument you’ve almost certainly played, or at least seen extended chords before even if you didn’t know that’s what they were or how they were formed. Chords like C7, Em7, AMaj9, Gm9 etc can sometimes seem a little daunting but these extended chords are usually only one or two notes more than the nice comfortable triads you’re already familiar with.
To form extended chords we take the same three notes as we would for a triad chord (R, 3, 5) and simply continue to count along the scale to include the necessary note(s) for the type of extended chord we are trying to find – 7th, 9th, 11th etc.
In taking these notes from the scale the chord originates from (if looking at a ‘D’ chord this would be the D Major scale) and seeing how they compare to the scale we are harmonizing we can see if any changes have occurred and form a formula for that chord enabling us to identify its type – Major, minor, dominant, diminished etc.
Let’s get stuck in and start harmonizing the C Major scale, this time with extended chords.
Step 1
For the purpose of continuity, we will continue using the C Major scale as our working example.
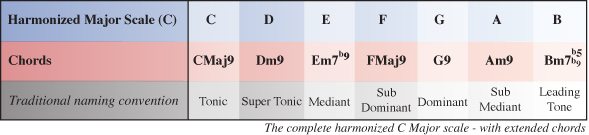
Below is the completed harmonized C Major scale using extended chords which is what we’ll be working towards in this part of the tutorial
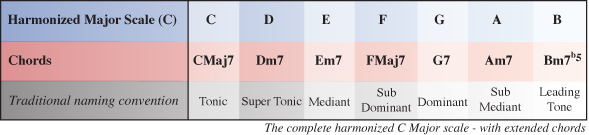
Download audio file (Step 1-Harmonized C Major Scale 7th.mp3)
Just as we did in part 1, we first need to write out all the notes of the Major scale we are harmonizing by using the Major scale formula: T, T, S, T, T, T, S. If you aren’t already familiar with this check out part 1 of this tutorial.
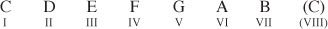
Step 2
As mentioned earlier, extended chords are chords that are made of four or more notes. To work out chord I of the C Major scale we now need to find the 1st, 3rd, 5th and 7th note to form a particultar type of extended C chord.

Because we are finding the root chord (in this case, a C chord within the key of C) all of the notes appear in their natural form with no alterations, so we can formularize chord I as R(1), 3, 5, 7 which is the formula for a Major 7 chord.
Chord I of the harmonized C Major scale is CMaj7 (C Major 7).
Step 3
Next we need to work out chord II of our Major scale. This is similar to the process we followed to find chord I only this time we start on the 2nd note of the scale (D) and count along to find the 3rd, 5th and 7th note to complete the extended D chord.
In the table below, you can see chord II starts with D as it’s root note (1), F as the 3rd note, A as the 5th note and C as the 7th note.

Now that we have the notes for a type of extended D chord, we need to compare these notes to the Major scale the D chord originates from – D Major.
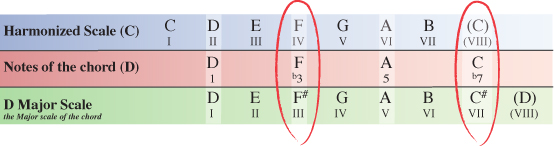
Comparing the notes of our D chord from within the harmonized C Major scale to the notes of the scale the chord originates or decends from you can see that two notes have been altered.
The 3rd note (F) and the 7th note (C) are both natural within C Major, whereas in the D Major scale they appear as F# and C#. Both notes have been flattened within the C Major scale and so we formularize our D chord as R(1), b3, 5, b7 which is the formula for a minor 7 chord.
Chord II of the harmonized C Major scale is Dm7 (D minor 7).
NOTE – Looking at the formula for each chord, you should already be able to see the difference between a Major7 and a minor7 chord. As we progress you’ll see some more chords and will eventually start to grasp the rules that apply to make each type of chord what it is ie Major7, minor7, Dominant7 etc
Step 4
Moving on, we now need to find out what chord III is.
Starting on the III degree of the C Major scale our next extended chord will have the note E as it’s 1st note (root note). Counting along the scale from this point the 3rd note is G, the 5th note is B and the 7th note is D.

Step 5
As we did in step 3 with the D chord, we now need to see how the notes of our E chord within the key of C Major compare to the same notes of the E Major scale which the chord originates from.
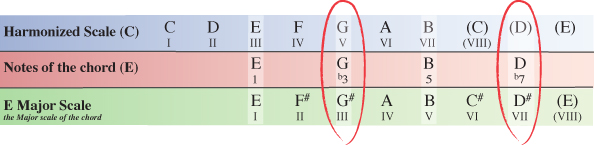
Our E chord from within the C Major scale has a G natural and a D natural, whereas the E Major scale which the chord originates from has a G# and D#. The 3rd and 7th notes of our E chord within C Major have been flattened, meaning we can formularize the extended E chord as 1, b3, 5, b7 which as we’ve already seen is the formula for any minor 7 chord.
Chord III of the harmonized C Major scale is Em7 (E minor 7).
Step 6
Next we’ll look at chord IV of the harmonized C Major scale.
Starting on the IV degree of the C Major scale our next chord will have the note F as it’s root note. Counting along the scale from this point the 3rd note is A, the 5th note is C and the 7th note is E.

Step 7
We now need to compare the notes of our extended F chord within the C Major scale to the same notes of the F Major scale which the chord originates from.

None of the notes of our F chord from within the C Major scale have been altered from how they appear in the F Major scale, so the F chord is simply formularized as 1, 3, 5, 7 which as we’ve already seen with chord I, is the formula for a Major 7 chord.
Chord IV of the harmonized C Major scale is FMaj7 (F Major 7).
Step 8
Next we’ll look at chord V of the harmonized C Major scale.
Starting on the V degree of the C Major scale our next chord will have the note G as it’s root note. Counting along the scale from this point the 3rd note is B, the 5th note is D and the 7th note is F.
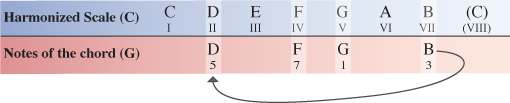
As in Part one of this tutorial, to save space in the following diagrams, we simply make use of the existing notes by cycling through back to the beginning of the scale and continuing to count along from there.
Step 9
We now need to compare the notes of our extended G chord within the C Major scale to the same notes of the G Major scale which the chord originates from.
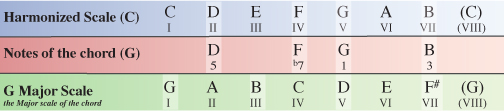
You’ll notice that only one of the notes within our G chord inside the C Major scale has been altered from how they appear in the G Major scale. We’ve already seen Major (natural) 3rds and minor (flattened) 7ths but not in the same chord. We can formularize our G (V) chord as R(1), 3, 5, b7 which is the formula for any Dominant 7 chord.
Chord V of the harmonized C Major scale is G7 (G Seven).
Step 10
Next up is chord VI of the harmonized C Major scale.
Starting on the VI degree of the C Major scale our next chord will have the note A as it’s root note. Counting along the scale from this point the 3rd note is C, the 5th note is E and the 7th note is G.
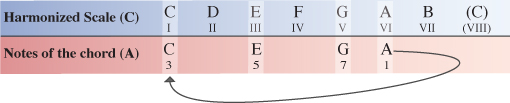
Step 11
We now need to compare the notes of our A chord within the C Major scale to the same notes of the A Major scale which the chord originates from.
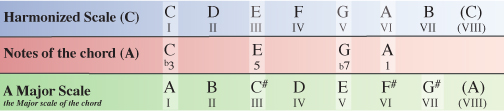
Comparing the extended A chord from within the C Major scale to the notes of the A Major scale we can see that the 3rd note and 7th note have again been flattened. In this case the 3rd note of the A chord has been flattened from a C# to a C natural and the 7th note of the A chord has been flattened from a G# to a G natural. This means our chord is formulated as 1, b3, 5, b7…another minor 7 chord.
Chord VI of the harmonized C Major scale is Am7 (A minor 7)
Step 12
Last but not least is chord VII of the harmonized C Major scale.
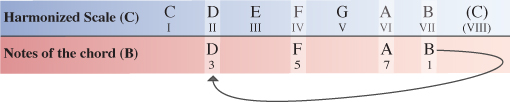
Starting on the VII degree of the C Major scale our final chord will have the note B as it’s root note. Counting along the scale from this point the 3rd note is D, the 5th note is F and the 7th note is A.
Step 13
Again, we need to compare the notes of our B chord within the C Major scale to the same notes of the B Major scale which the chord originates from.
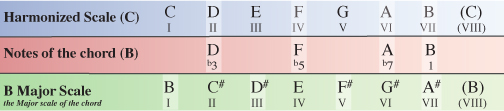
Once again, the VII degree of the harmonized Major scale is the odd ball. You can see that, with the exception of the root note, every note of the B chord within the C Major scale has been flattened from how it appears naturally in the B Major scale.
This means we formularize our B chord as R(1), b3, b5, b7. While you might think this is simply Bdiminished7, it is actually what’s known as a half-diminished chord which can also commonly be written as Bm7b5 (B minor 7, flat 5) or Bø.
The reason for calling this chord a half-diminished (or Bm7b5) is to make a clear distinction between a true diminished seventh chord which is a diminished triad plus a diminished 7th (R, b3, b5, bb7) and a diminished triad plus a minor 7th (R, b3, b5, b7).
Taking our B chord as the example, Bdim7 (B diminished 7th) would have the notes B, D, F, Ab while Bm7b5 or Bø has the notes B, D, F, A. The key difference is that a diminished 7th is a 7th note with two flat signs (double flat) which means we lower the note by 2 semi-tones as apposed to a minor 7th which is a 7th note with just one flat sign and therefore is only lowered by one semi-tone.
So finally, the extended chord VII of the harmonized C Major scale is Bm7b5 or Bø.
Step 14
While we’ve only covered 7ths for the most part of our working example, the process to go even further to include 9, 11 or 13 chords is just the same only you are often dealing with more notes.
If for example I wanted to know what the 9 chords would be, I could continue to count along the notes of the C Major scale to find that extra note, bringing the 9 into my chord as well as the R(1), 3, 5 and 7.
To get you started, lets take a quick look at how we might do the first couple of chords

You can see here that for chord I of the C Major scale, I have all the same notes that were used in my CMaj7 chord earlier. The only difference is I have now gone one step further to include the 9 as well.
This time, the formula for chord I is R(1), 3, 5, 7, 9 which is the formula for a CMaj9 (C Major 9) chord.
Step 15
Following the same process for chord II of the C Major scale our D chord will be formularized as R(1), b3, 5, b7, 9 which is the formula for a m9 (minor 9) chord.
So chord II of the harmonized C Major scale is Dm9 (D minor 9).
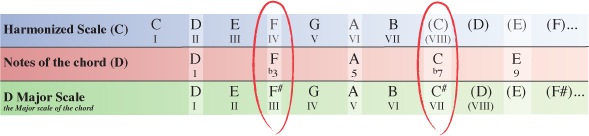
Below is the complete harmonized C Major scale using 9 chords.
Download audio file (Step 15-Harmonized C Major Scale 9th.mp3)
Conclusion
I hope this has helped you to feel much more confident with regards to what is going on within Major key signatures and how the chords from a given key are derived. Not only that but it also reveals how different types of chords are formed. For instance, a minor chord always has a b3 (minor 3rd/flattened 3rd), a 7 chord always has a b7 (minor 7th/flattened 7th) etc.
When you start looking at scales in this way you really start to understand what’s going on below the surface. You will notice some interresting relationships between different chords and will have a much deeper understanding of how to emphasize or even just imply chord tones by the notes you choose to use in your improvizing or when composing melodies.
For writing chord progressions you realize you’re no longer limited to plain Major or minor triad chords. You can exploit the much deeper, richer tonalities of extended chords from the safety of your newly discovered knowledge of the key you are using.
The key to really feeling comfortable with the ideas in this tutorial is regular exposure. Practice harmonizing different Major scales and try doing it with different types of chords ie triads, 7 chords, 9 chords, 11 chords etc.
Also, when you’re playing or writing your own music try to visualize the chord that is being played and which notes you could use either from that chord or notes you could play in addition to that chord thereby ‘implying’ the extended chord tones – 7th, 9th, 11th etc.