The Harmonized Major scale enables us to identify all the chords within a given key. Not only does this make it much quicker and easier to find the right chords when writing or playing music, it is also extremely important to understand which key you are in for the improvisation of melodies and solos.
Step 1
Below is the completed harmonized Major scale, which we will be working out for ourselves in this turorial:
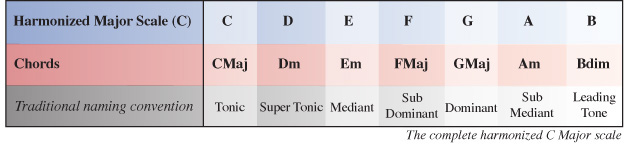
Download audio file (Harmonized C Major Scale.mp3)
First of all, we need to write out all the notes within the scale/key we are trying to harmonize (C Major in this case). If you don’t already know which notes belong to the scale you can use the Major scale formula to count the interval between notes in Tones (T) and Semi-Tones (S) starting on the root note of the scale: T, T, S, T, T, T, S

Step 2
Now we have the available notes in our key we can start working out which chords fall on each degree of the scale (I, II, III, IV etc) by taking each note in the scale as a root note (1) for each chord. By counting along the scale starting on each root note we can pick the 3rd and 5th notes from that point to form the rest of the chord.
Let’s start with chord I which takes the note C as its root note. C is the root note (1st note) of the chord. E will be the 3rd note of the chord and G will be the 5th note of the chord. When comparing these notes to the scale/key of the chord (C), which in the case of the root chord will be the same scale/key we are harmonizing, we have a 1, 3, 5 which is the formula for any Major chord. So chord I of the harmonized C Major scale is C Major.

Step 3
Next we need to work out chord II of our Major scale. This is similar to the process we followed to find chord I only this time we start on the 2nd note of the scale (D) and count along to find the 3rd and 5th note to complete the chord.
In the table below, you can see chord II starts with D as its root note (1), F as the 3rd note and A as the 5th note.

Now we have the notes for a type of D chord, but we need to investigate a little further in order to find out exactly which type of D chord it is – Major, minor, Diminished etc.
To do this we take the notes of the chord from the scale we are harmonizing and compare them with the Major scale the chord itself originates from, which in this case is D Major.
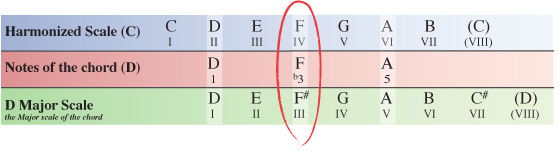
Here you can see the note F within C Major, and in turn within our D chord is natural (not a sharp or flat), whereas the D Major scale has an F#. So when comparing our D chord to it’s scale of origin (D Major), the F# has been flattened to an F natural meaning the third note of our chord has become a flattened 3rd (b3) within the key of C Major.
The 1st and 5th note of the chord are the same in both keys and so remain unchanged.
Knowing this, we can formularize our D chord as 1 b3 5 (one, flat 3, 5) which is the formula of any minor chord, meaning the II chord within the key of C Major is Dm (D minor).
NOTE – Although we are finding chords within the C Major scale, we view the notes of the chords within this key from the perspective of the scale they originate from, so a C chord from the perspective of C Major, a D chord from the perspective of D Major, an E chord from the perspective of E Major and so on.
This way you will see which notes from the key you are using, if any, have been altered from their natural state.
Step 4
You’ll be pleased to know we’re now over the hardest part. Working out the rest of the chords for the Harmonized C Major scale follows the same processes taken in steps 2 and 3.
Let’s push on then and find out what chord III is.
Starting on the III degree of the C Major scale our next chord will have the note E as its 1st note (root note). Counting along the scale from this point the 3rd note is G and the 5th note is B.

Step 5
As we did in step 3 with the D chord, we now need to see how the notes of our E chord within the key compare to the same notes of the E Major scale which the chord originates from.
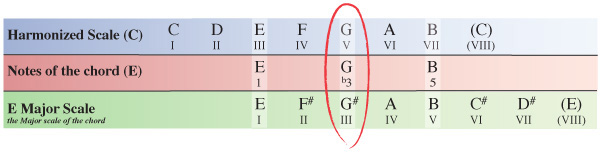
Our E chord from within the C Major scale has a G natural, whereas the E Major scale which the chord originates from has a G#. The 3rd note of our E chord within C Major has been flattened from a G# (in E Major) to a G natural meaning we can formularize the E chord as 1, b3, 5 which as we’ve already seen is the formula for any minor chord.
Chord III of the harmonized C Major scale is Em (E minor).
Step 6
Next we’ll look at chord IV of the harmonized C Major scale.
Starting on the IV degree of the C Major scale our next chord will have the note F as its root note. Counting along the scale from this point the 3rd note is A and the 5th note is C.

Step 7
As before, we now need to compare the notes of our F chord within the C Major scale to the same notes of the F Major scale which the chord originates from.
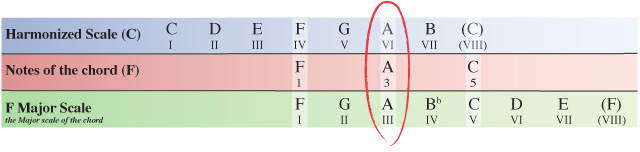
You’ll notice here that none of the notes within our F chord inside the C Major scale have been altered from how they appear in the F Major scale so the F chord is simply formularized as 1, 3, 5 which as we’ve already seen is the formula for a Major chord.
Chord IV of the harmonized C Major scale is F (F Major).
Step 8
Next we’ll look at chord V of the harmonized C Major scale.
Starting on the V degree of the C Major scale our next chord will have the note G as its root note. Counting along the scale from this point the 3rd note is B and the 5th note is D.
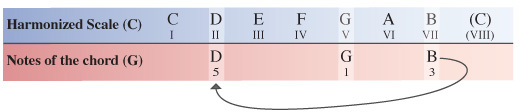
In the previous diagrams, the notes of the scales and chord are matched up vertically to make things easier to see.
To save space in the following diagrams, we simply make use of the existing notes by cycling through back to the beginning of the scale and continuing to count along from there.
Step 9
We now need to compare the notes of our G chord within the C Major scale to the same notes of the G Major scale which the chord originates from.
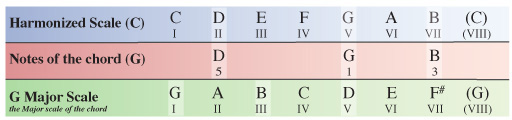
None of the notes within our G chord inside the C Major scale have been altered from how they appear in the G Major scale so the G chord is again formularized as 1, 3, 5.
Chord V of the harmonized C Major scale is G (G Major).
Step 10
Next up is chord VI of the harmonized C Major scale.
Starting on the VI degree of the C Major scale our next chord will have the note A as its root note. Counting along the scale from this point the 3rd note is C and the 5th note is E.
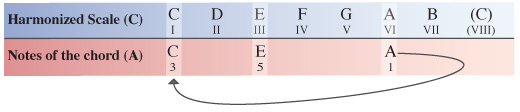
Step 11
We now need to compare the notes of our A chord within the C Major scale to the same notes of the A Major scale which the chord originates from.
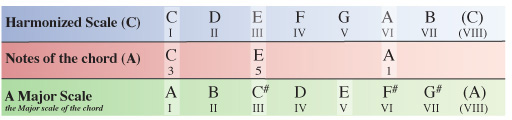
Comparing the A chord from within the C Major scale to the notes of the A Major scale we can see that the 3rd note has again been flattened. In this case the 3rd note of the A chord has been flattened from a C# to a C natural leading to our chord to being formulated as 1, b3, 5 – another minor chord.
Chord VI of the harmonized C Major scale is Am (A minor)
Step 12
Last but not least is chord VII of the harmonized C Major scale.
Starting on the VII degree of the C Major scale our final chord will have the note B as its root note. Counting along the scale from this point the 3rd note is D and the 5th note is F.
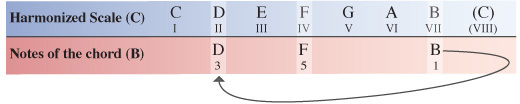
Step 13
We now need to compare the notes of our B chord within the C Major scale to the same notes of the B Major scale which the chord originates from.
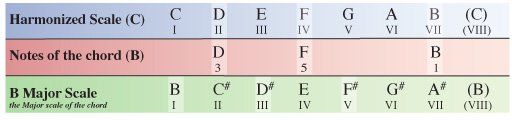
This time, comparing the B chord from within the C Major scale to the notes of the B Major scale we can see something a little different from the chords we’ve encountered so far.
The 3rd note has again been flattened, but this time the 5th note has also been flattened from a F# within the B Major scale to a F natural within the chord from our C Major scale.
This means we formularize the chord as 1, b3, b5 which is the formula for a diminished chord. So in this case, chord VII of the harmonized C Major scale is Bdim (B diminished)
Conclusion
While this may seem like a lengthy process at first, it’s actually quite simple once you’ve had a few goes at it.
Practice by harmonizing any other Major scale: A, D, E, F for example. If you work through a couple each week or better yet, every day, you’ll soon be doing it with ease and in half the time!
Through regular practice you’ll be able to identify intervals between notes better and you will start to recognize Major or minor tones of chords within the scales you are using when playing over different chord progressions, helping you to avoid the bad notes and really capitalize on the great ones!
In the second part of this tutorial we will be looking at how you can expand on the harmonized Major scale even further to make use of extended chords.